ALGEBRA 2º ESO

TEMA 5. EXPRESIONES ALGEBRAICAS. 

Made with Storyboard That CONOCIMIENTOS PREVIOS: ÁLGEBRA_1ºESO by Esther Pg on Scribd

CONTENIDOS:

1.- Expresiones algebraicas

2.- Valor numérico de una expresión algebraica.

1.- Expresiones algebraicas

Una expresión algebraica es una expresión matemática en la que intervienen letras, números y los signos de operaciones aritméticas.

Las letras reciben el nombre de variables o  indeterminadas y representan números o cantidades desconocidas.

Ejemplos: a) v=d/t

                     b) 2x-1

En matemáticas Las expresiones algebraicas se nombran con una letra mayúscula y, entre paréntesis, las variables que intervienen en la expresión.

Ejemplos: A(x)=2x2−3x+12

• $\mathrm{B(x},y)=\frac{2x^2-3}{x{y}^2}$

El valor numérico de una expresión algebraica es el resultado obtenido al sustituir cada una de las variables por números.

Ejemplos: a) Consideremos la fórmula de la velocidad:              

                        v=d/t

                    Si d=18; t=6, entonces: v=d/t =18/6=3

                 b) Sea la expresión 2x-1

Para x=0, tenemos: 2·0-1 = -1

Para x=1, tenemos 2·1-1 = 2 – 1 = 1

Para x=10, tenemos 2· 10 -1=19 

       c) Sea la expresión: el 30% de espectadores

  pondremos, 30% de x, o bien  0,3x

Si los espectadores son 80, entonces: 0,3·80=24  

d) Dado A(x)=2x2−3x+12, calcula el valor de A(x) para x=2.

 

-Utilidad del lenguaje algebraico:

Permite expresar cualquier situación de la vida real por medio del lenguaje matemático utilizando para ello expresiones matemáticas

EJEMPLOS:

a) El doble de la edad de Javier más la de su hermano es la edad de su padre.

Edad de Javier: j

Edad del hermano: h

Edad del padre: p

Entonces: p = 2·(j+h) 

-Si Javier tiene 8 años y su hermano 10. ¿Qué edad tiene el padre? 

               p = 2 · (10+8) = 2 ·18 = 36

-Si Javier tiene 8 años y el padre 40. ¿Cuál es la edad del hermano? 

Como la edad de Javier y su hermano es la mitad de la edad del padre. Divido 40 entre 2, sale 20. Por lo tanto la edad del hermano es h = 20 – 8 =12

RELACIÓN ENTRE ENUNCIADO Y EXPRESIONES ALGEBRAICAS:

Practica:

 1.- Lenguaje algebraico

Concepto del Polinomio y Monomio

Empezemos con el monomio:

Un monomio es una expresión algebraica en la que se utilizan letras, números y signos de operaciones. Las únicas operaciones que aparecen entre las letras son el producto y la potencia de exponente natural. Se denomina polinomio a la suma de varios monomios. Un monomio es un polinomio con un único término.

EJEMPLOS:::

          18xy

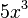
7

Elementos de un monomio

• coeficiente: Los números, si no tiene número el coeficiente es 1.
• parte literal: las letras. A cada una de las letras se le llama variables.
EJEMPLO::::::
Dado el monomio 

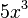
• coeficiente: ______ 
• parte literal: ______

El coeficiente de un monomio es el número que aparece multiplicando a la parte literal. Normalmente se coloca al principio. Si tiene valor 1 no se escribe, y nunca puede ser cero ya que la expresión completa tendría valor cero.

Grado de un monomio

El grado de un monomio es el número de factores de la parte literal, se calculasumando los exponentes de las variables (letras) que lo componen.

Ejemplos

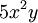tiene grado 3 

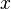tiene grado 1 

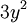tiene grado 2 

VALOR NUMÉRICO DE UN MONOMIO

Polinomio:

Polinomio, en matemáticas, se denomina a la suma de varios monomios, llamados términos del polinomio. Es una expresión algebraica constituida por una o más variables, utilizando solamente operaciones de adición, sustracción, multiplicación y exponentes numéricos positivos. El polinomio de un sólo término se denomina monomio, el de dos binomio, el de tres trinomio.

Notaremos los polinomios con las letras mayúsculas P, Q, R, S, etc.

por ejemplo:

Se denomina GRADO de un polinomio a la mayor potencia de los monomios que lo componen.

A cada uno de los sumandos del polinomio lo llamaremos TÉRMINOS DEL POLINOMIO.

Al término del polinomio sin letra, se le llama TÉRMINO INDEPENDIENTE.
Polinomio completo si tiene todos los términos iguales o menores a su grado.
Polinomio incompleto si le falta alguno de los términos inferiores a su grado.
ORDENAR términos.
AGRUPAR términos.

Monomios, binomios, trinomios

Hay nombres especiales para los polinomios con 1, 2 o 3 términos:

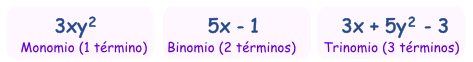
¿Cómo te aprendes los nombres? ¡Piensa en bicicletas!

(También existen cuatrinomio (4 términos) y quintinomio (5 términos), pero se usan poco) 

SUMA Y RESTA DE POLINOMIOS:
Se realiza igual que en la suma y resta de monomios con paréntesis.
EJEMPLO:  (2x² + 6y + 3xy)  +   (3x² - 5xy - x) 



Para RESTAR polinomios, primero invierte el signo de cada término que vas a restar (en otras palabras cambia "+" por "-", y "-" por "+"), después suma normalmente.
(2x² + 6y + 3xy)  -   (3x² - 5xy - x) 

Sumar varios polinomios utilizando columnas.

Puedes sumar varios polinomios juntos así.

Ejemplo: suma     (2x² + 6y + 3xy)  ,   (3x² - 5xy - x)   y   (6xy + 5)

Ponlos alineados en columnas y suma:

2x² + 6y + 3xy
3x²      - 5xy - x
           6xy     + 5

5x² + 6y + 4xy - x + 5

NOTA: Debes poner los términos semejantes unos encima de otros. Y si en alguno de los polinomios no aparece un término dejar el espacio.

Restar polinomios usando columnas (2x² + 6y + 3xy)  -   (3x² - 5xy - x) 

Cambio de signo el monómio que aparece con el signo menos:

2x² + 6y + 3xy
-3x²      + 5xy + x
                    

-x² + 6y + 8xy + x

MULTIPLICACIÓN DE polinomios

ver disfruta de las matemáticas .com

MULTIPLICACIÓN EN VERTICAL
EJEMPLO 2: (Multiplicación de polinomios completos)
paso 1: ordeno y completo los polinomios, pongo uno debajo del otro.

paso 2, 3, 4, ...: multiplico  cada término del 2º polinomio por todos los miembros del primer polinomio.

paso último: sumo los polinomios resultantes.
A = 4x³ - 5x² + 2x + 1
B = 3x - 6

                4x³ - 5x² + 2x +  1   (el polinomio A ordenado y completo)

              X                  3x  -  6  (el polinomio B ordenado y completo)

EJEMPLO 3: (Multiplicación de polinomios incompletos y desordenados, completándolos y ordenándolos) A =  -9x2 + x + 5x4 B = 3 - 2x2                           5x4 + 0x3 - 9x2 + x + 0         (completo y ordenado)             X                         -2x2 + 0x + 3         (completo y ordenado)            ______________________________ paso 2: multiplico por 3 (del 2º monomio) todos los miembros del primer monomio. paso 3:multiplico por _____ todos los miembros del primer monomio                        paso 4: multiplico por _____todos los miembros del primer monomio                       ________________________________________ Paso 5: sumo los polinomios resultantes:  -10x6 +  0x5 + 33x4 - 2x3 - 27x2 + 3x + 0 RESULTADO: A x B =  -10x6 + 33x4 - 2x3 - 27x2 + 3x EN DEFINITIVA:                           5x4 + 0x3 - 9x2 + x + 0         (completo y ordenado)             X                         -2x2 + 0x + 3         (completo y ordenado)            ______________________________                      15x4 + 0x3 - 27x2 + 3x  + 0              0x5 +  0x4 + 0x3 +  0x2 +  0x   -10x6 + 0x5 + 18x4 - 2x3 + 0x2 ________________________________________  -10x6 +  0x5 + 33x4 - 2x3 - 27x2 + 3x + 0 A x B =  -10x6 + 33x4 - 2x3 - 27x2 + 3x EJEMPLO 4. ejercicios página.... NOTA:::::Es posible resolver sin necesidad de poner los 0 utilizando el siguiente truco::::

A =  -9x² + x + 5x⁴
B = 3 - 2x² 


                         5x⁴ - 9x² + x             (incompleto pero ordenado)

             X                -2x² + 3              (incompleto pero ordenado)
            _____________________
              15x⁴        - 27x² + 3x

   -10x⁶ + 18x⁴ - 2x³ 
 ____________________________ 
   -10x⁶ + 33x⁴ - 2x³ - 27x² + 3x



A x B =  -10x⁶ + 33x⁴ - 2x³ - 27x² + 3x
VIDEOS

EJERCICIOS INTERACTIVOS: ver enlace

IDENTIDADES NOTABLES.
ver video


 TEORIA MONOMIOS

operaciones con monomios from moises12septiembre
ELEMENTOS DE UN MONOMIO-SUMA Y RESTA

MULTIPLICACIÓN Y DIVISIÓN DE MONOMIOS
METODO DE LA BALANZA:

 VIDEO ELEMENTOS Y PROPIEDADES:





EXPRESIONES ALGEBRAICAS BY TRONCHO:

LENGUAJE ALGEBRAICO. IR A JUEGO

DONALD EN EL PAIS DE LAS MATEMATICAS:

SISTEMAS DE ECUACIONES
http://matematicas2esojafr.blogspot.com.es/2012/03/fichas-de-sistemas-de-ecuaciones.html