-Expresiones algebraicas.
-Suma, diferencia y producto de polinomios
-Potencia de un polinomio. Identidades notables.
-División de polinomios.
-Regla de Ruffini.
-Teorema del resto y del factor.
-Raíces de un polinomio. Factorización.
SUMA, DIFERENCIA Y PRODUCTO:
SUMA, DIFERENCIA
MONOMIOS
|
A(x)
|
B(x)
|
A(x)+B(x)
|
A(x)-B(x)
|
No semejantes
|
-5x2
|
2x4
|
2x4-5x2
|
-5x2-(2x4)= -5x2-2x4=
-2x4-5x2
|
Semejantes: Se suman coeficientes, se conserva la parte
literal
|
-5x2
|
7x2
|
-5x2+ 7x2=
(-5+7)x2
|
-5x2-(7x2)=-5x2-7x2=
(-5-7) x2=-12x2
|
POLINOMIOS
|
P(x)
|
Q(x)
|
P(x)+Q(x)
|
|
SUMA:Reduzco
el polinomio, agrupando términos semejantes.
|
2x4-5x2
|
6x5-3x4+2x2-4x+1
|
2x4-5x2+6x5-3x4+2x2-4x+1=
|
|
RESTA
|
P(x)-Q(x)
|
|||
1º Quito paréntesis, si delante hay un “-“ cambio de signo
todo el polinomio.
2º Reduzco el
polinomio
|
2x4-5x2+6x5-(-3x4+2x2-4x+1)=
|
|||
PRODUCTO
MONOMIOS
|
A(x)·B(x)
|
Resultado.
|
Multiplico
los coeficientes. Multiplico la parte literal sumando los exponentes.
|
(-5x2)·( 2x4)=
|
(-5·2)·( x2·x4)= -10x6
|
MONOMIO POR POLINOMIO
|
A(x)·Q(x)
|
|
Multiplico el
monomio por cada término del polinomio.
|
(-5x2)( 2x4-3x2+2x-6)
|
(-5x2)( 2x4-3x2+2x-6)
|
POLINOMIOS.
|
P(x)·Q(x)
|
|
Multiplico
cada término del primer polinomio por cada término del segundo.
|
IDENTIDADES NOTABLES.
CUADRADO DE LA SUMA
|
(a+b) 2=
|
Ejemplo.
|
El cuadrado
del primero más el doble del primero por el segundo más el cuadrado del
segundo.
|
a2+2ab+b2
|
( x2+2)2=
|
CUADRADO DE LA RESTA
|
(a-b) 2=
|
|
El cuadrado
del primero más el doble del primero por el segundo menos el cuadrado del
segundo.
|
a2-2ab+b2
|
( 3x2-4)2=
|
SUMA POR DIFERENCIA
|
(a+b)·(a-b)
|
|
El cuadrado
del primero menos el cuadrado del segundo.
|
a2-b2
|
(5x2+2y) (5x2-2y) =
|
Ejemplos:
DIVISIÓN
Ejemplos:
REGLA DE RUFFINI: Permite realizar de
forma rápida la división de un polinomio entre un binomio (POLINOMIO DE GRADO
2) del tipo x+a o x-a, donde a es un número real positivo.
Ejemplo, consideremos P(x)=2x3 + x2 - 3x + 5 y Q(x)=x-1. La división se realiza como sigue:
 1.Se ordena el polinomio P(x) de mayor a menor grado y se colocan los coeficientes de cada término . Si no apareciese algún término entre el de mayor grado y el de menor se coloca un 0. A la izquierda se pone el número que se resta a x en Q(x), en nuestro caso 1 y se baja el coeficiente del término de mayor grado, este paso se corresponde con la figura 1.
1.Se ordena el polinomio P(x) de mayor a menor grado y se colocan los coeficientes de cada término . Si no apareciese algún término entre el de mayor grado y el de menor se coloca un 0. A la izquierda se pone el número que se resta a x en Q(x), en nuestro caso 1 y se baja el coeficiente del término de mayor grado, este paso se corresponde con la figura 1.2. Se multiplica el coeficiente que se ha bajado (2) por el que se ha colocado a la izquierda (1). El resultado del producto se coloca debajo del coeficiente del término siguiente y se suman. Figura 2
3. El resultado de la suma se vuelve a multiplicar por el número situado a la izquierda y se repite el proceso. Figuras 3 y 4.
4. El último número (recuadro rojo en Fig. 4) se corresponde con el resto de la división mientras que el resto de números de la fila inferior son los coeficientes del cociente.
Resto = 5 y C(x)=2x2 + 3x por tanto 2x3 + x2 - 3x + 5 =(x-1) (2x2 + 3x) +5
TEOREMA DEL RESTO Y DEL FACTOR
Enunciado
|
APICACIONES
|
|
TEOREMA DEL RESTO
|
El resto de dividir un polinomio P(x) entre el binomio x-a es igual al valor numérico
del polinomio para x=a
|
-Permite calcular el valor numérico x=a simplemente aplicando
RUFFINI.
-Permite determinar el resto de la división
P(x):(x-a) calculando el valor para P(a) obtenemos el resto. Es decir P(a)=R(x)=RESTO |
TEOREMA DEL FACTOR
|
Un polinomio P(x) tiene como factor x-a (es divisible por x-a) si
el valor numérico del polinomio para x=a es cero; es decir P(a)=0
A LOS NÚMERO QUE HACEN ESTO SE LES LLAMA RAICES DEL POLINOMIO.
|
-Permite calcular las raices de un polinomio aplicando Ruffini.
-Permite descomponer factorialmente un polinomio calculando sus
raices.
|
TEOREMA FUNDAMENTAL
DEL ÁLGEBRA
|
Un polinomio de grado n puede tener, como máximo, n raices
reales.
|
-Permite conocer el número máximo de divisores del polinomio
conociendo su grado.
-Además, los valores de a, son múltiplos del término independiente.
|
- EJERCICIO: Ver solución >>
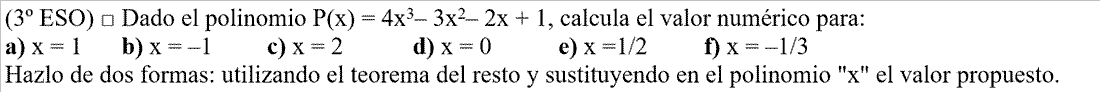
- EJERCICIO: Ver solución >>
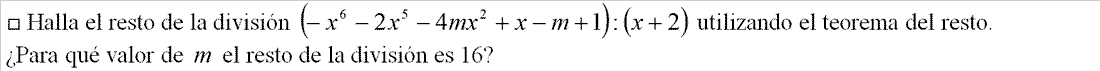 EJERCICIO: Ver solución >>
EJERCICIO: Ver solución >>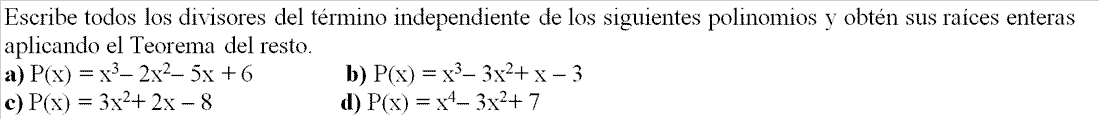
- EJERCICIO: Ver solución >>
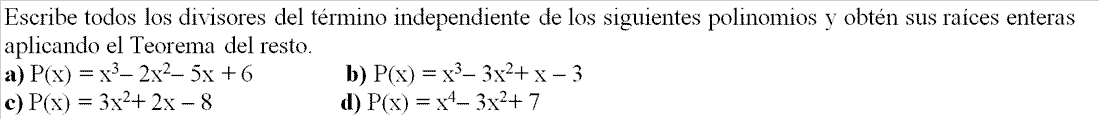
- EJERCICIO: Ver solución >>
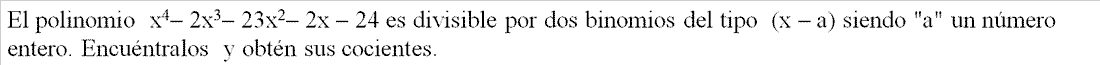
- EJERCICIO: Ver solución >>
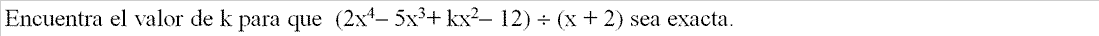
- EJERCICIO: Ver solución >>
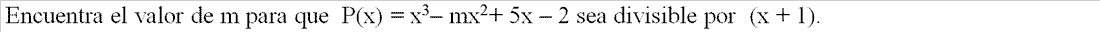
- EJERCICIO: Ver solución >>
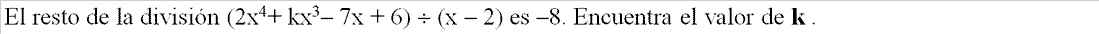
- EJERCICIO: Ver solución >>

FACTORIZACIÓN, es descomponer un polinomio P(x) en todos los factores de la forma (x-a) o (x+a) posibles.Ejemplo: P(x)=4·(x-2)·(x-3)·(x+5)·(x-5)·(3x-1)Para poder expresarlo así utilizaremos Ruffini, y la resolución de ecuaciones de segundo grado. - EJERCICIO: 1ª parte - 2ª parte
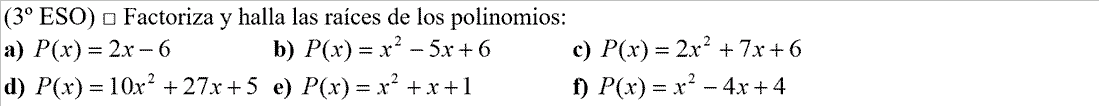
- EJERCICIO: 1ª parte - 2ª parte - 3ª parte
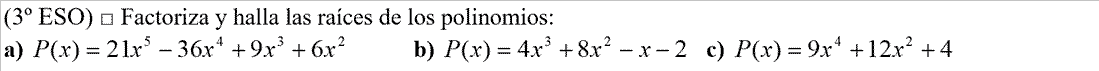
- EJERCICIO: Ver solución >>
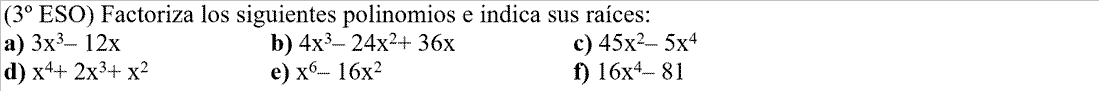
- EJERCICIO: Ver solución >>
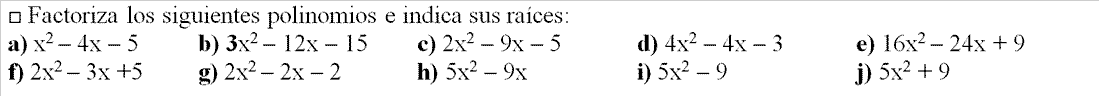
- EJERCICIO: Ver solución >>:
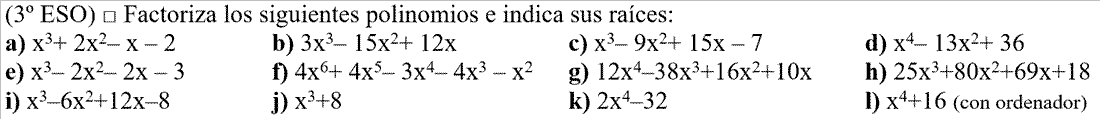
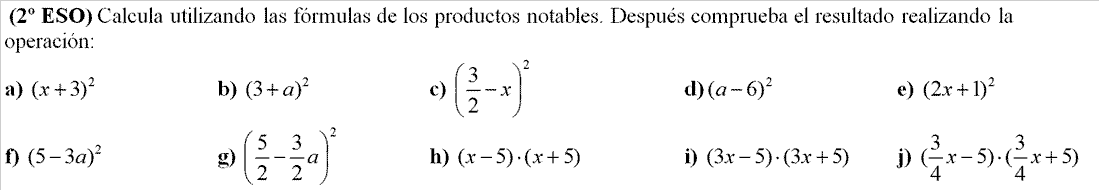
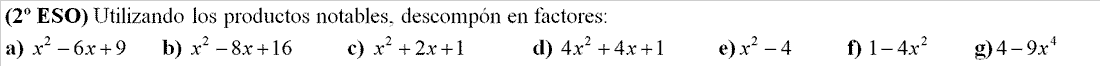
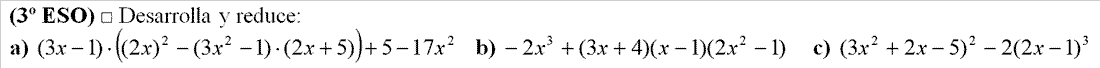
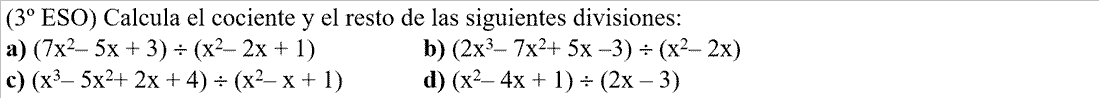
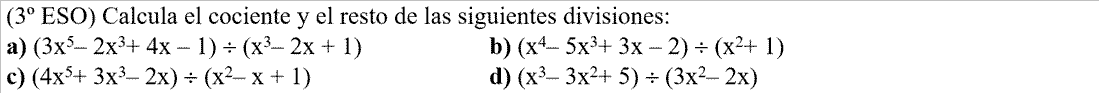
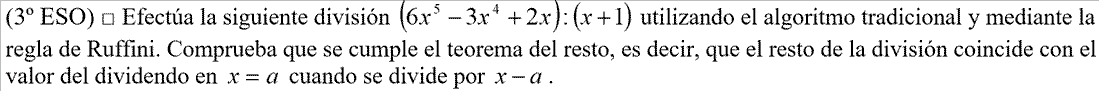
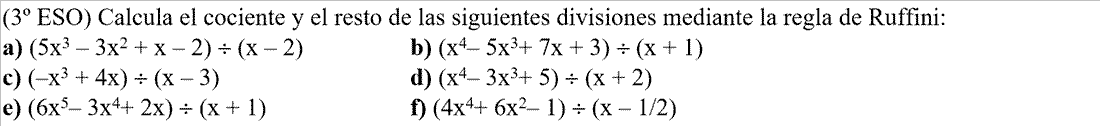
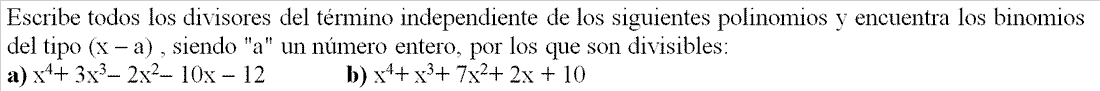
No hay comentarios:
Publicar un comentario